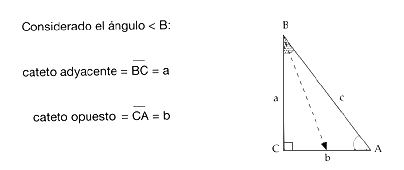
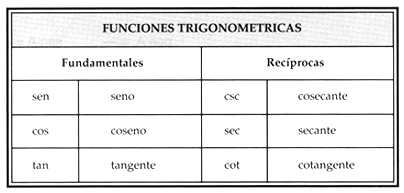
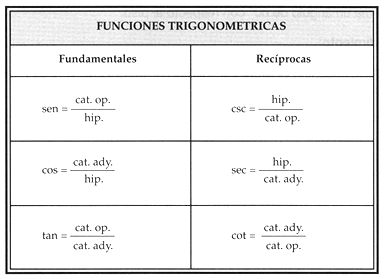
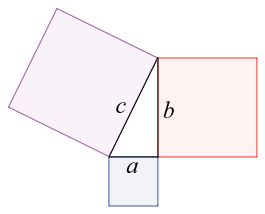
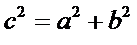Para que puedan resolver los problemas del cuadernillo de actividades de las páginas 14 y 15 observen estos ejemplos, mismos que les serán útiles más adelante.
Ejemplos:
1.-Obtención del valor de un lado, conocidos un ángulo y un lado
Obtener la longitud de una escalera recargada en una pared de 4.33 m de altura que forma un ángulo de 60° con respecto al piso.
Procedimiento:
a) Trazar el triángulo rectángulo anotando los datos e indicando, con una letra, el lado que se desea calcular.
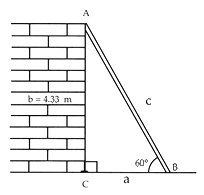
b) Seleccionar una razón trigonométrica que relacione al ángulo y lado conocidos con el lado que se desea calcular.

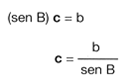
c) Despejar algebraicamente la letra que representa el lado que se desea calcular.
d) Sustituir las literales por sus valores numéricos de acuerdo con los datos.

e) Obtener el valor natural del ángulo por medio de las tablas trigonométricas o de la calculadora y efectuar las operaciones.

c = 5 m
f) Dar solución al problema.
c = longitud de la escalera
Por lo tanto, la escalera mide 5 m.
2. Obtención del valor de un ángulo agudo, conocidos dos lados del triángulo
Obtener el ángulo que forma un poste de 7.5 m de alto con un cable tirante que va, desde la punta del primero hasta el piso, y que tiene un largo de 13.75 m
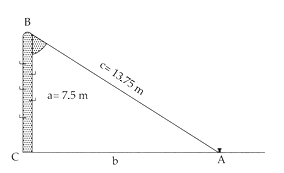
Ahora se tienen únicamente los valores de dos lados, con los cuales se debe obtener el valor del ángulo.
Procedimiento:
a) Trazar un triángulo rectángulo anotando en el los datos.
b) Seleccionar la función trigonométrica que relacione a los lados conocidos con el ángulo.

c) Sustituir las literales por sus valores numéricos.

d) Efectuar la división indicada.
cos = 0.5454
e) Obtener, en las tablas de funciones trigonométricas o con la calculadora, el valor del ángulo.

f) Dar respuesta al problema.
El ángulo formado por el poste y el cable tirante es de 56° 57′
- Para resolver algunos problemas, donde se aplica la trigonometría, es conveniente conocer lo que es un ángulo de elevación y un ángulo de depresión.
Ángulo de elevación
El ángulo O, formado por la horizontal OM y la visual ON situadas en el mismo plano vertical es el ángulo de elevación del punto N, que es, a su vez, el punto más elevado del objeto.

Ángulo de depresión

El ángulo B, formado por la horizontal BD y la visual BA situadas en el mismo plano vertical, es el ángulo de depresión del punto A.
Nótese que:

a) <β y <α son congruentes por ser ángulos alternos internos entre paralelas.
b) <β y <γ son complementarios porque sus medidas suman 90°.
c) Triángulo ABC es congruente con el triángulo ABD.
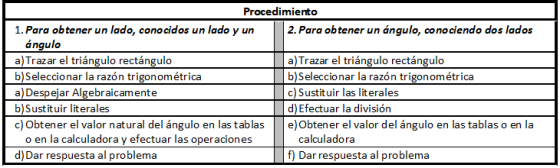
En el siguiente cuadro se resumen los dos procedimientos para la resolución de triángulos rectángulos
Actividad para entregar el día 16 de Mayo de 2012, realizada en el cuaderno.
1. Una escalera de mano está apoyada contra la pared de un edificio. Del pie de la escalera al edificio hay 12 m. La escalera forma con el suelo un ángulo de 70°. Halla la longitud de la escalera y la altura respecto del suelo del extremo superior de la citada escalera.
2. Un árbol proyecta una sombra de 18 m sobre el plano horizontal en que está situado, cuando los rayos del sol inciden con un ángulo de 20°. Halla la altura del árbol.
3. Una cometa está unida al suelo por un hilo de 100 m, que forma con un terreno llano un ángulo de 55°. Suponiendo que el hilo está tirante, halla a qué altura, respecto del suelo, está la cometa.
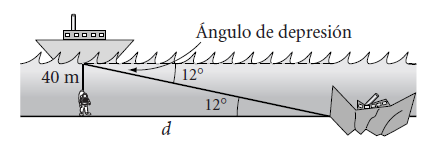
4. El sonar de un barco de salvamento localiza los restos de un naufragio en un ángulo de depresión de 12°. Un buzo es bajado 40 metros hasta el fondo del mar. ¿Cuánto necesita avanzar el buzo por el fondo para encontrar los restos del naufragio?
5. Un árbol de hoja perenne está sostenido por un alambre que se extiende desde 1.5 pies debajo de la parte superior del árbol hasta una estaca en el suelo. El alambre mide 24 pies de largo y forma un ángulo de 58° con el suelo. ¿Qué altura tiene el árbol?

6. En los ejercicios 1 a 3, asocia la razón trigonométrica con su definición.

1. tan R 2. cos R 3. sen R
7. Usa un transportador para dibujar un triángulo con medidas de ángulo de 40°, 50° y 90°. Mide los lados con una regla. Luego, usa tus medidas para aproximar el seno, el coseno y la tangente de 40°.
8. Usa un transportador para dibujar un triángulo con ángulos de 40°, 50° y 90° que sea más grande que el del ejercicio 4. Mide los lados y luego usa tus medidas para aproximar el seno, el coseno y la tangente de 40°. ¿Obtienes los mismos resultados que en el ejercicio 4?
9. En los ejercicios 6 a 11, usa la siguiente figura Δ XYZ para hallar la razón trigonométrica.
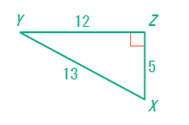
6. sen X 7. cos X
8. tan X 9. sen Y
10. cos Y 11. tan Y
10. En los ejercicios 12 a 17, usa Δ DEF para hallar la razón trigonométrica.

12. sen D 13. cos D
14. tan D 15. sen E
16. cos E 17. tan E
11. En los ejercicios 18 a 21, resuelve el ángulo y el lado no rotulado de cada triángulo. Luego, escribe seis razones trigonométricas que puedan formarse con cada triángulo.
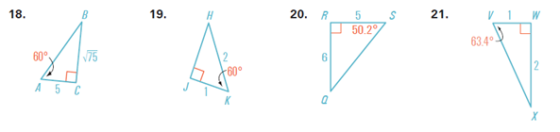
12. En los ejercicios 22 y 23, dibuja un triángulo rectángulo, Δ ABC, que tenga las razones trigonométricas dadas. Rotula cada lado con su longitud.

13. Halla las razones trigonométricas de los ángulos agudos de los triángulos rectángulos indicados a continuación
a) 5, 4 y 3 cm b) 8, 10 y 6 cm c) 5, 12 y 13 cm d) 16, 34 y 30 cm
14. En un triángulo rectángulo ABC la hipotenusa a = 14 y el seno B= 0,75. Resuelve el triángulo.
15. En un triángulo rectángulo ABC el cateto b = 14 y el seno C= 0,68. Resuelve el triángulo.
16. En un triángulo rectángulo ABC la hipotenusa a = 84 y la tangente B= 1,25. Resuelve el triángulo.
17. En un triángulo rectángulo ABC el cateto c = 64 y la tangente B= 1,25. Resuelve el triángulo.
18. En un triángulo rectángulo ABC el cateto b = 64 y el coseno C = 0,32. Resuelve el triángulo.
19. Calcula las restantes razones trigonométricas de los ángulos α , b , m y r sabiendo que
a) sen α = 4/7 b) cos b = 1/3 c) tg m = 7/6 d) tg r = 1/2
20. Halla las razones trigonométricas de los ángulos de 30° y de 60°. Ayúdate de los triángulos equiláteros.
21. Halla las razones trigonométricas del ángulo de 45°. Ayúdate de un cuadrado.
22. Calcula la longitud de la sombra de un abeto de 24 m de altura cuando la inclinación de los rayos del sol sea 23°.
23. Los extremos de las ramas de un compás distan 6 cm y cada rama mide 14 cm. Halla el ángulo que forman las dos ramas.